Multi fidelity surrogates¶

Single fidelity surrogates such as Kriging model already showed incredible performance on expensive black-box function problems. However, for extremely expensive problems, the single fidelity surrogates may not be able to provide accurate prediction results due to the lack of samples. Commonly, we can easily get low-fidelity samples for the same problem, those low-fidelity samples is much cheaper but less accurate than the high-fidelity samples.

To make use of those low-fidelity samplers to enhance the prediction accuracy, multi-fidelity surrogates are proposedMulti-fidelity GPs were initially developed by O’Hagan in the 1990s [1]. The author considered an auto-regressive model and demonstrated the potential of reaching similar accuracy to conventional GPs while requiring less computational time. Other multi-fidelity formulations have been proposed as well, but multi-fidelity GPs can be roughly categorized in two groups:

Auto-regression models and their extensions, like Co-Kriging model [1]

Scaling-based multi-fidelity GPs [2]

Others, like Hierarchical Kriging model [3]

Note

By the following, the basic of Co-Kriging model will be briedly introduced, and for the details of other multi-fidelity surrogates, please refer to the original papers.

Co-Kriging model¶

1. basics of Co-Kriging model¶

The idea of auto-regression model can be expressed by [4] , which can be expressed as:

\[f_h \left ( \boldsymbol{x} \right) = \boldsymbol{\rho} f_l \left ( \boldsymbol{x} \right) + f_d \left ( \boldsymbol{x} \right)\]

where the high-fidelity GP \(f_h \left ( \boldsymbol{x} \right)\) is the summation of two GPs (the low-fidelity \(f_l \left ( \boldsymbol{x} \right)\) and the difference \(f_d \left ( \boldsymbol{x} \right)\)), and where \(\boldsymbol{\rho}\) is an additional hyper-parameter to control the correlation level between high-fidelity and low-fidelity. The auto-regression model expands the covariance matrix to the form of

\[\begin{split}\mathcal{C} = \begin{pmatrix} \mathcal{K} \left( \boldsymbol{x}_h, \boldsymbol{x}_h \right) & \mathcal{K} \left( \boldsymbol{x}_h, \boldsymbol{x}_l \right)\\ \mathcal{K} \left( \boldsymbol{x}_l, \boldsymbol{x}_h \right) & \mathcal{K} \left( \boldsymbol{x}_l, \boldsymbol{x}_l \right) \end{pmatrix}\end{split}\]

2. Training and Inference¶

The training of Co-Kriging model consists of two stages. In the first stage, we can train a low fidelity Kriging model GaussianProcessRegression based on the low-fidelity samples. Then, combine the low-fidelity Kriging model and the high-fidelity samples, we can train a discrepancy Kriging model, and finding the best \(\boldsymbol{\rho}\).

Implementation¶

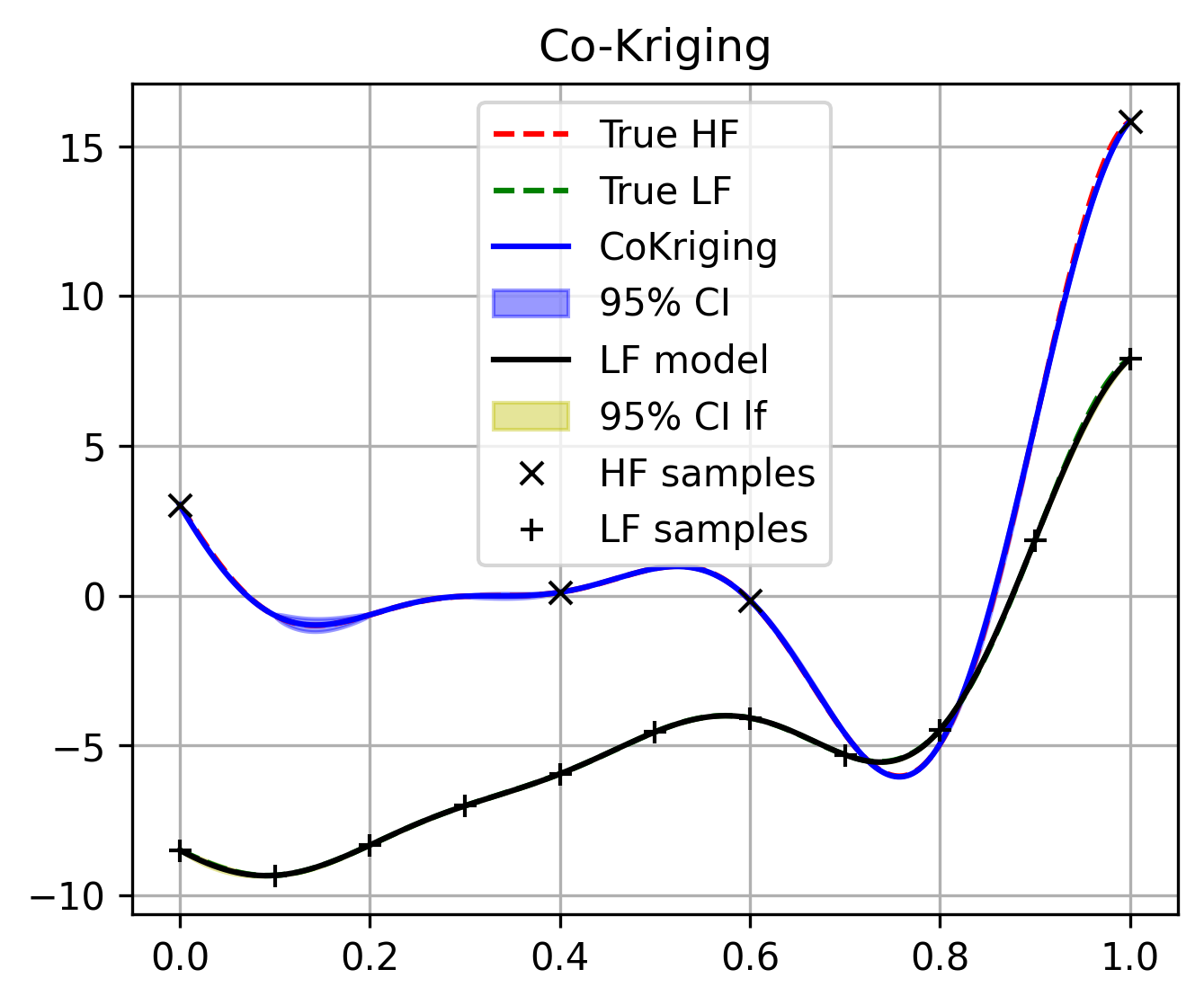
The Co-Kriging model is implemented in CoKriging class. The following example is given to illustrate the usage of the how to train and predict with Co-Kriging model:

# Import required libraries
import matplotlib.pyplot as plt
import numpy as np

# Import necessary modules
from mfpml.design_of_experiment.mf_samplers import MFSobolSequence
from mfpml.models.co_kriging import CoKriging
from mfpml.problems.mf_functions import Forrester_1b

# Step 1: Define the Multi-Fidelity Function
func = Forrester_1b()

# Step 2: Generate Samples at Two Fidelity Levels
sampler = MFSobolSequence(design_space=func._input_domain, num_fidelity=2)
sample_x = sampler.get_samples(num_samples=[10, 100], seed=2)
sample_y = func(sample_x)

# Add noise to the samples
np.random.seed(2)
sample_y[0] += np.random.normal(0, 0.3, sample_y[0].shape)  # Low-fidelity noise
sample_y[1] += np.random.normal(0, 0.3, sample_y[1].shape)  # High-fidelity noise

# Step 3: Generate Test Data
test_x = np.linspace(0, 1, 1000).reshape(-1, 1)
test_hf_y = func.hf(test_x)  # High-fidelity ground truth
test_lf_y = func.lf(test_x)  # Low-fidelity ground truth

# Step 4: Train the Co-Kriging Model
coK = CoKriging(design_space=func._input_domain, optimizer_restart=10, noise_prior=None)
coK.train(sample_x, sample_y)

# Step 5: Predictions
cok_predictions, cok_std = coK.predict(test_x, return_std=True)

# Step 6: Plot the Results
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(test_x, test_hf_y, "r--", label="True High-Fidelity")
ax.plot(test_x, test_lf_y, "g--", label="True Low-Fidelity")
ax.plot(test_x, cok_predictions, "b-", label="Co-Kriging Predictions")
ax.fill_between(
    test_x[:, 0],
    cok_predictions[:, 0] - 1.96 * cok_std[:, 0],
    cok_predictions[:, 0] + 1.96 * cok_std[:, 0],
    alpha=0.4,
    color="b",
    label="95% Confidence Interval",
)
ax.scatter(sample_x[0], sample_y[0], color="green", label="Low-Fidelity Samples")
ax.scatter(sample_x[1], sample_y[1], color="red", label="High-Fidelity Samples")
ax.legend(loc="best")
ax.grid("--")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Multi-Fidelity Co-Kriging Regression")
plt.show()

# Step 7: Print Training Information
print(f"Low-Fidelity Training Time: {coK.lf_training_time:.4f} seconds")
print(f"High-Fidelity Training Time: {coK.hf_training_time:.4f} seconds")

Implemented multi-fidelity surrogates¶

Multifidelity surrogate	API of sampling methods
Co-Kriging	`CoKriging`
Hierarchical Kriging	`HierarchicalKriging`
Scaled Kriging	`ScaledKriging`